Theme: Islamic astronomy
- InfoVersion: 2
Status: PUB
Date: 2017-11-09 13:21:54
Author(s): Tofigh Heidarzadeh
In the time interval between Ptolemy (2nd century AD) and Copernicus (16th century), the major developments in observational and theoretical astronomy took place from North Africa to Central Asia—during late Antiquity, and then in pre-Islamic and finally Islamic societies. The main advances happened between the 9th and the mid-15th centuries. During this period, Muslim scholars familiarized themselves with Indo-Persian astronomical traditions, mastered Ptolemaic planetary models, improved computational and observational techniques, established large-scale observatories, devised accurate observational instruments and, finally, developed several non-Ptolemaic planetary models to make the observed motions of planets more compatible with Aristotelian cosmology.
The introduction of Hellenistic astronomy - InfoVersion: 15
Status: PUB
Date: 2017-11-09 14:30:06
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Our knowledge about the extent of peoples’ familiarity with astronomy in the Arabian Peninsula in pre-Islamic times is limited. However, it is known that they were familiar with the sun’s journey through the zodiacal signs, and that they adopted a lunar calendar, defined lunar mansions by identifying certain fixed stars and asterisms, and used the rising and setting times of certain specific stars to predict seasonal and meteorological phenomena.
The rapid expansion of the Islamic territories from the mid-7th century onwards put Muslims in contact with Persians and Byzantines who had a long tradition in astronomy. However, Muslims’ acquaintance with ‘foreign’ sciences, including astronomy, really began in the late 8th century when the first translations of Greek, Syriac and Persian works into Arabic became available in the court of the ‘Abbasid caliph, al-Mansūr, in the newly built capital city of Baghdad. The establishment of the House of Wisdom, an institute for research and translation, in the early 9th century in Baghdad led to the start of the great project of translating scientific and philosophical books from the Greek, Hellenistic, Persian, and Indian traditions.
Before long, thanks to the translation of works such as the Persian Zīj-i Shahriyār (translated into Arabic as Zīj al-Shāh), the Sindhind (Indian astronomical tables in Sanskrit), Ptolemy’s Mathematikē Sýntaxis (Mathematical Treatise, commonly called Almagest, based on the Latin form of its Arabic title, Kitab al-Majistī, The Great Book), and other mathematical works from the Greek and Hellenistic traditions, Muslims became familiar with planetary models and mathematical astronomy. However, it was Ptolemaic astronomy that finally became dominant among Muslim astronomers, although preparing zījs based on the Indo-Persian tradition also continued. During the 8th and 9th centuries, Ptolemy’s Almagest was translated at least five times into Arabic, and his other works—most importantly the Planetary Hypothesis—also became known to astronomers practising in the Islamic territories. When the main texts became available, several commentaries, critical revisions, and summaries also appeared. Some of these discussed the difficulties and inconsistencies found in the original texts, while others helped to make them comprehensible to students.
Muslims’ first introduction to computational astronomy was through the zījs. A zīj is a combination of tables consisting of observational data about the motion and position of the planets, sun, moon, and certain fixed stars, and the coordinates of the points of intersection of major circles in the celestial sphere, which enabled astronomers and astrologers to make their astronomical calculations and predictions. The term is derived from the Middle Persian word zīk or zīg, meaning cord.
The first zījs produced in the Islamic period were based on the Indo-Persian tradition: Zīj al-Arkand was written in Arabic in the year 735 based on Indian tables; Zīj-i Shahriyār was translated from Pahlavi in the final years of the 8th century (Muslim astronomers knew it in the Pahlavi original long before its translation); and Zīj al-Sindhind was translated from Sanskrit in the 770s by al-Fazārī and Ya‘qūb ibn Tāriq, the court scholars of the ‘Abbasid caliph al-Mansūr. However, in the first half of the 9th century al-Khwārizmī, a Persian mathematician and astronomer who lived in Baghdad, compiled a zīj, which is the first extant original Islamic astronomical table. Although elements from the previously translated tables are used in this zīj, Ptolemaic elements were also introduced. The zīj was written under the patronage of caliph al-Ma‘mūn, during whose reign (813-33) Ptolemy’s Almagest was twice translated into Arabic.
Mixing parameters from the Indian-Iranian and Ptolemaic tables, as was done in al-Khwārizmī’s zīj and other similar tables, would have created disparities both in practical and predictive astronomy. On the other hand, more than six centuries had elapsed since the time of Ptolemy, during which period the parameters of positional astronomy had altered anyway, so the early Islamic observational astronomers’ struggle with the observational discrepancies was inevitable anyway. The earliest efforts at observational astronomy included attempts to build instruments based on information from Ptolemy and other sources, and to measure some of the basic parameters of positional astronomy such as the obliquity of the ecliptic, the length of the solar year and the length of a degree of latitude, as well as certain lunar parameters. Muslim astronomers also performed observations to fix local coordinates in order to determine the qibla—the sacred direction of Mecca—towards which Muslims face when praying. Through these observational programs, astronomers were able to correct errors found in the ancient observations, and to obtain updated values for astronomical parameters. This helped them avoid using contradictory parameters from different sources.
During al-Ma‘mūn’s reign, other observational programs started in Baghdad and Damascus. New parameters were calculated for the solar, lunar, and planetary motions; the obliquity of the ecliptic was measured; and observations took place to determine the positions of stars. Astronomers also performed geodesic measurements to determine the size of the earth by measuring the length of a degree of latitude (in order to provide a new map of the world), and fixed local coordinates by simultaneous observations of a lunar eclipse from Baghdad and Mecca, in order to determine the qibla in Baghdad. The outcome of these diverse observations was (directly or indirectly) influential in providing new zījs, among them al-Zīj al-Mumtahan and the zīj of Habash al-Hāsib. In these tables, not only were new values used for astronomical parameters; new computational techniques were also employed, as one can see from the use of new spherical trigonometry in the zīj of Habash al-Hāsib. In addition, the comparison of the results of these observations with those from the Hellenistic period led to important corrections to the existing kinematic models. For instance, it was established that, contra Ptolemy and Hipparchus, the position of the solar apogee with respect to the vernal equinox was not fixed.
This observational tradition persisted after al-Ma‘mūn. Among the astronomers of the second half of the 9th century was Thābit ibn Qurra (836-901), a polymath and the editor of an Arabic translation of Ptolemy’s Almagest. Thābit was a Sābian from Harran (now in southern Turkey). Sābians were the followers of an ancient religious order who worshipped the heavenly bodies. Thābit carefully observed the motions of the sun and the moon, measured the length of the sidereal year, determined the solar apogee and eccentricity, and wrote the Book on the Solar Year, On the Visibility of the New Moon, and a book concerning the apparent motion of the moon based on Ptolemy’s lunar theory. Thābit also concluded that the precession of the equinoxes was not linear, but rather that it was oscillating periodically. He explained this theory of the trepidation of the equinoxes in his treatise On the Motion of the Eighth Sphere. Thābit proposed that the poles of the eighth sphere were moving on small circles whose centres held the poles of a ninth sphere.
A contemporary of Thābit, the astronomer al-Battānī or Albategnius in its Latinized form (c. 850-929), observing from a city located on the north bank of the Euphrates, calculated a new figure for the obliquity of the ecliptic (23° 35′ instead of Ptolemy’s 23° 51′ 20″), found an accurate value for the eccentricity of the sun (0.017326 instead of Ptolemy’s 0.0175), observed the planetary motions carefully, and improved the observed values for the moon’s mean motion in longitude. In his zīj (known as al-zīj al-Sābi‘ī) al-Battānī not only used improved values for most of the planetary parameters, but also employed new formulae in spherical trigonometry. In addition, he introduced revised or new types of observational instruments, such as a new sundial, an armillary, and a mural quadrant. Al-Battānī, for the first time in the history of astronomy, talked about the possibility of solar annular eclipses, which he deduced from the variations in the apparent sizes of the moon and the sun.
By the beginning of the 11th century, attempts to perform accurate observations, hand in hand with the development of new methods in mathematical astronomy, became a characteristic feature of Islamic astronomy: the astronomers concerned include ‘Abd al-Rahmān al-Sūfī (903-86), Abū‘l Wafā al-Būzjānī (d. c. 997), Ibn Yūnus (d. 1009), and Abū Rayhān al-Bīrūnī (973-1048). The Persian al-Sūfī, in his Book of Fixed Stars (964)—which was the first complete survey of the night sky since Ptolemy—provided an accurate star catalogue with corrections to the positional data and magnitudes in Ptolemy’s star list. He also described a number of nebulous objects which we now categorize as galaxies and star clusters. Abū‘l Wafā, another Persian astronomer and mathematician, worked mostly on mathematical astronomy and made significant developments in spherical astronomy. By introducing new methods, Abū‘l Wafā made the solution of problems involving oblique spherical triangles simpler and more accurate than using Ptolemy’s methods, which were based on the Theorem of Menelaus. Ibn Yūnus, observing in Cairo, prepared an excellent zīj (called the Hakīmī Zīj) which differed from other extant zījs by exhibiting the author’s knowledge of his predecessors’ observations and his awareness of observational errors and computational precision. His tables for timekeeping were still being used in Cairo in the 19th century. The multi-disciplinary scholar al-Bīrūnī not only introduced a sophisticated spherical trigonometry to solve astronomical and geodesic problems, but also attempted to re-measure some of the astronomical parameters and local coordinates.
Meticulous observations such as these became an integral part of astronomy in the Muslim world throughout the following centuries. However, this was not the main contribution of Islamic astronomy. Major developments also occurred in the fields of theoretical and mathematical astronomy. Some of these developments were triggered by practical needs relating to astronomical and geodesic problems in Islamic rituals, while others were theoretical and philosophical in nature. In both aspects, astronomers in the Islamic territories made significant progress in the history of astronomy.
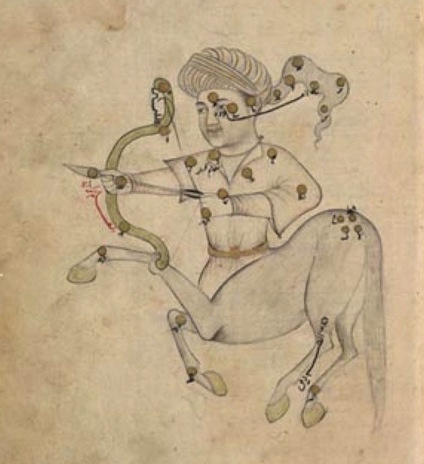
Fig. 1. A page from al-Sūfī’s star catalogue: the constellation Sagittarius as seen on a celestial globe. From ‘Abd al-Rahmān al-Sūfī (Azophi) (964), Book of Fixed Stars. Creative Commons Licence

Fig. 2. Zīj Gurgani [Zīj-i Jurjānī = Gurgani Astronomical Tables]. 1193 H/1779. Beinecke Rare Book & Manuscript Library. (Public domain)
- InfoVersion: 2
Status: PUB
Date: 2012-04-13 21:40:04
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Practical astronomy
The astronomical and geodesic issues relating to Islamic rituals can be discussed under three headings: problems related to timekeeping; the determination of the sacred direction (qibla); and the regulation of the lunar calendar. The exact times of the five daily prayers are based on the position of the sun in the sky: the times of the daylight prayers are determined by the length of shadows, while the times of prayers when the sun is not above the local horizon are established on the basis of twilight phenomena. The morning prayer begins at dawn and ends before sunrise; the noon prayer starts at noon, after the sun crosses the local meridian and the shadow of a vertical object reaches its minimum; the next prayer starts in the afternoon, when the length of the shadow of any object is equal to the sum of its midday minimum shadow and the length of the object casting the shadow; the next prayer starts after the afternoon prayer and ends before sunset; and the final prayer starts when the afterglow disappears and should end before midnight. Although it is not difficult to estimate these prayer times empirically, to determine them accurately one needs to acquire a good knowledge of the local coordinate system and the day-to-day changes in the apparent position of the sun in the sky.
During the first thirteen years of the rise of Islam, Muslims faced Jerusalem while praying. However, seventeen months after the Hijra—the migration of the prophet Muhammad from Mecca to Medina—the orientation of prayers (qibla) changed so as to be towards the Kaaba in Mecca. Since Mecca is located south of Medina, finding the qibla in Medina was not difficult. However, once the Islamic territories expanded, finding the right qibla became a challenging problem in spherical geometry. The problem was to find the direction of the great circle passing through two points on the globe. Over the centuries, Muslim astronomers and mathematicians developed methods to solve this problem based on spherical trigonometry, and produced tables and even sophisticated instruments to find the orientation of Mecca from different locations.
The regulation of the lunar calendar was one of the most important and at the same time one of the most difficult problems for Muslim astronomers. In Islamic sacred law, the lunar month starts with the first sighting of the new crescent moon. Depending on the time that has elapsed since new moon, this first crescent can be very tricky to observe, owing to the short time it stays above the horizon and its faint glow compared to the brightness of the western horizon after sunset. Therefore, one needs to know exactly when and where to look to find the first crescent. Traditionally, observers were sent to locations with an open horizon to report on the visibility of the moon. If they failed to see it, they would need to repeat their observations the next evening. If the horizon was cloudy, fixed number of days had to be assumed for the month in question. These uncertainties, especially for the holy month of Ramadan, were problematic. Early Muslim astronomers, based on Indian sources, developed procedures to define the visibility of the new crescent by calculating the relative distances of the sun and the moon and working out the difference in their setting times. However, in the centuries that followed they developed more complex procedures, taking into account also the angular separation of the sun and the moon and the apparent velocity of the moon, and provided complicated tables to determine the visibility.
- InfoVersion: 8
Status: PUB
Date: 2012-04-13 22:05:54
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Observatories
In order to obtain accurate celestial data for both astronomical and astrological purposes, continuous observational programs were a necessity. While some data can be obtained in a relatively short time with portable instruments, most of the data needed in positional astronomy require long-term observations. As a result, the establishment of observatories became an integral part of astronomical programmes in the Islamic period. According to available sources, the first observatories in Islam were established in Baghdad and Damascus under the patronage of the ‘Abbasid caliph al-Ma‘mūn in the early 9th century. These observatories, which have not survived, were mainly established so as to update the values of astronomical and geodesic parameters in order to compile new zījs, to prepare accurate tables for timekeeping and calendar regulation, and to produce new star maps.
Some scholars made observations independently of al-Ma‘mūn’s observatories, using their own private observational stations. For example, al-Battānī observed for many years in Raqqa (in northern Syria); the Banū Mūsā brothers observed for about thirty years from their own properties in Baghdad and the nearby city of Samarra; the Banū Amājūr family, including the father, two sons, and a freed slave, observed over a long period and made their own zījs; and Sharf al-Dawla built an observatory in the garden of his palace in Baghdad.
From the mid-10th to the mid-13th century, observatories or observational stations were built all over the Islamic territories, with various observational instruments and to perform different astronomical programs. In the 950s al-Sūfī conducted observations in Rayy (near Tehran) and Shiraz; in the late 10th century Abū‘l Wafā al-Būzjānī observed from Baghdad, and observed a lunar eclipse simultaneously with al-Bīrūnī while the latter was in Khwarizm (in modern Turkmenistan); in 994 al-Khujandī measured the obliquity of the ecliptic in Rayy using a sextant about 20m in radius; in the 970s Ibn Yūnus started an extended observational program in Cairo which he explains in his zīj; in the late 10th century and the first two decades of the 11th century al-Bīrūnī conducted observations for more than thirty years in Khurasan (eastern Iran); in the late 11th century ‘Umar al-Khayyām used an observatory in Isfahan, Iran, for about 18 years where he prepared a zīj and supervised the calendar reform project for the Seljuk ruler, Malik Shāh; and finally Sā ‘id al-Andalusī and Ibn al-Zarqāllu undertook a long-term observational program in Spain in the 11th century.
However, two observatories in the Islamic period occupy a special place in the history of astronomy: the Maragha Observatory, built in 1259 in northern Iran under the patronage of Hūlāgū (a grandson of the Mongol conqueror Genghis Khan); and the Samarqand Observatory, founded by Ulugh Beg (a grandson of Tamerlane) in 1424. The scale of the observational instruments in these two observatories, the importance of their observational programmes, their institutional setting, and the number of affiliated astronomers and mathematicians, combine to make these two institutions unique in the history of medieval astronomy.
The Samarqand observatory, which was based upon ideas from the Maragha Observatory, in turn became a model for an observatory built by Taqī al-Dīn in Istanbul in 1575 and the Jantar Mantar observatories in north India in the 1720s. After the fall of Ulugh Beg’s dynasty in the 1450s, a number of scholars in Ulugh Beg’s circle emigrated to the newly born Ottoman Empire, where they strongly influenced scientific developments. Taqī al-Dīn, the court astronomer of Sultan Murad III (reign 1574-95), established an observatory in Istanbul, something the Turkish Sultans had dreamed of ever since they conquered Constantinople in 1453. About fifteen astronomers helped to build and use the instruments, whose purpose was to produce a new zīj. However, after two years the great comet of 1577 appeared, which Taqī al-Dīn interpreted as a sign that the Turkish army would be victorious against Persia. Although the Persian army was defeated in the war, the Turkish troops also suffered heavy losses. In the same year several dignitaries died within short intervals, and there was also a plague. Referring to these unpredicted horrifying events, the Sultan believed that the comet appeared because of the establishment of the observatory and that it would go away if its cause (the observatory) were removed. As a result, the observatory was demolished at once, before Taqī al-Dīn was able to finalize his zīj.
The Jantar Mantar observatories built by Jai Singh in northern India between 1724 and 1734, although built after the invention of the telescope, continued the Islamic-Persian tradition of monumental observatory building and were greatly inspired by the Samarqand Observatory.
- InfoVersion: 21
Status: PUB
Date: 2017-11-10 06:46:56
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Theoretical astronomy
In addition to observational and computational astronomy, Muslim astronomers had a special interest in creating a clear picture of the universe in its physical sense. It was generally accepted that the earth was located at the centre of the universe, with all celestial bodies moving uniformly around it. Aristotle had argued that the celestial region consisted of a series of concentric spheres (or ‘orbs’) with the earth at the centre. Each of the planets, for example, moved at a constant rate around one of these orbs. However, observational data did not support this picture: all celestial bodies from the sun and the moon to the planets and stars manifested different short-term or secular non-uniform motions. To explain these observations, non-concentric models of planetary motions had been developed in the 3rd and 2nd centuries BC, culminating in Ptolemy’s model of the planetary motions. This preserved the concentric orbs but included other eccentric orbs and epicycles embedded in each orb. According to Ptolemy, the uniform motion of a planet or the centre of an epicycle occurred around a point called the equant which did not coincide with the earth. With this innovation, the observations and the mathematical models of the planetary motions became compatible, but the physical structure of the universe became unclear. The problem was simple: given that the eccentric orbs, epicycles and equant were only mathematical devices to make the planetary motions calculable, what was the true physical configuration of the celestial spheres? Even Ptolemy was not explicit in his treatment of the universe: in the Almagest he merely describes the motions and models mathematically, while in his Planetary Hypothesis he talks about the configuration of the spheres without referring to problematic premises that underlie his mathematical models.
Critiques of Ptolemy started to appear soon after Muslim astronomers became familiar with the Ptolemaic system. Doubts concerning either Ptolemy’s observational data or his description of the cosmos became common in Islam. The main challenge was to create a configuration (hay‘a) of the universe that satisfied both observational and physical principles. The main goal, in other words, was to develop models involving uniform motions around the centre of the universe—the earth—that were compatible with observations.
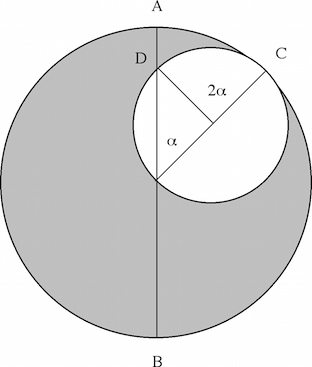

Fig. 3. Left/Top: Tūsī’s couple. Imagine two spheres internally tangent at one point (C), the diameter of the small sphere being equal to half of the other. If the small sphere uniformly moves twice (2α) as fast as the big sphere but in the opposite direction, the common point D will move back and forth along AB. In other words, the uniform circular motions of the two spheres create a linear motion. By choosing a Tūsī’s couple with the right dimensions and speeds of the two revolving spheres, and attaching it to a given sphere, one can produce the observed non-uniform motion of a particular planet around the central earth, even though the motion of the revolving spheres is uniform. Therefore, both observation and physical principles are preserved. © Tofigh Heidarzadeh. Right/Bottom: Tūsī’s diagram of the couple, showing the oscillation of a given point along the diameter of the big circle. After Tūsī couple from Vat. Arabic ms 319, commons.wikimedia.org. Creative Commons Licence
Solving this problem occupied the minds of several Muslim astronomers, among them Ibn al-Haytham, Ibn-Sīnā’s student Abū ‘Ubeyd Jūzjānī, Ibn Rūshd, and Ibn Bājja. However, it was Nasīr al-Dīn al-Tūsī who developed a revolutionary solution to eliminate the equant. Tūsī introduced an arrangement in which the circular motions of two spheres produced a linear motion displacing a point (for example the centre of an epicycle) closer to or further from a central point. This arrangement (called Tūsī’s couple), which was able to produce non-uniform motions from concentric uniform motions, was a key concept in the development of non-Ptolemaic models. Tūsī’s contemporaries Mu‘ayyad al-Dīn al-‘Urdī and Qutb al-Dīn Shīrazī also developed innovative non-Ptolemaic models, and the tradition continued with further models produced by Alī Al-Qūshjī (of Samarqand Observatory) and Ibn al-Shātir (1304-75), the timekeeper of the Umayyad Mosque in Damascus.
Copernicus repeatedly used concepts developed by Tūsī and his followers and colleagues. In De revolutionibus he employed Tūsī’s couple to create the variation in the obliquity of the ecliptic and to produce an oscillation in the orbital planes of planets. In the Commentariolus Copernicus uses al-‘Urdī and Ibn al-Shātir’s models to develop his own models for planetary longitude. Copernicus’s model for the lunar motions is almost the same as the model proposed by Ibn al-Shātir. Copernicus probably became aware of Muslim non-Ptolemaic models, especially those developed by Tūsī and his followers, when he was studying in Italy, where there was easier access to Arabic texts.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.
- InfoVersion: 2
Status: PUB
Date: 2017-11-09 13:21:54
Author(s): Tofigh Heidarzadeh

In the time interval between Ptolemy (2nd century AD) and Copernicus (16th century), the major developments in observational and theoretical astronomy took place from North Africa to Central Asia—during late Antiquity, and then in pre-Islamic and finally Islamic societies. The main advances happened between the 9th and the mid-15th centuries. During this period, Muslim scholars familiarized themselves with Indo-Persian astronomical traditions, mastered Ptolemaic planetary models, improved computational and observational techniques, established large-scale observatories, devised accurate observational instruments and, finally, developed several non-Ptolemaic planetary models to make the observed motions of planets more compatible with Aristotelian cosmology.
The introduction of Hellenistic astronomy - InfoVersion: 15
Status: PUB
Date: 2017-11-09 14:30:06
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Our knowledge about the extent of peoples’ familiarity with astronomy in the Arabian Peninsula in pre-Islamic times is limited. However, it is known that they were familiar with the sun’s journey through the zodiacal signs, and that they adopted a lunar calendar, defined lunar mansions by identifying certain fixed stars and asterisms, and used the rising and setting times of certain specific stars to predict seasonal and meteorological phenomena.
The rapid expansion of the Islamic territories from the mid-7th century onwards put Muslims in contact with Persians and Byzantines who had a long tradition in astronomy. However, Muslims’ acquaintance with ‘foreign’ sciences, including astronomy, really began in the late 8th century when the first translations of Greek, Syriac and Persian works into Arabic became available in the court of the ‘Abbasid caliph, al-Mansūr, in the newly built capital city of Baghdad. The establishment of the House of Wisdom, an institute for research and translation, in the early 9th century in Baghdad led to the start of the great project of translating scientific and philosophical books from the Greek, Hellenistic, Persian, and Indian traditions.
Before long, thanks to the translation of works such as the Persian Zīj-i Shahriyār (translated into Arabic as Zīj al-Shāh), the Sindhind (Indian astronomical tables in Sanskrit), Ptolemy’s Mathematikē Sýntaxis (Mathematical Treatise, commonly called Almagest, based on the Latin form of its Arabic title, Kitab al-Majistī, The Great Book), and other mathematical works from the Greek and Hellenistic traditions, Muslims became familiar with planetary models and mathematical astronomy. However, it was Ptolemaic astronomy that finally became dominant among Muslim astronomers, although preparing zījs based on the Indo-Persian tradition also continued. During the 8th and 9th centuries, Ptolemy’s Almagest was translated at least five times into Arabic, and his other works—most importantly the Planetary Hypothesis—also became known to astronomers practising in the Islamic territories. When the main texts became available, several commentaries, critical revisions, and summaries also appeared. Some of these discussed the difficulties and inconsistencies found in the original texts, while others helped to make them comprehensible to students.
Muslims’ first introduction to computational astronomy was through the zījs. A zīj is a combination of tables consisting of observational data about the motion and position of the planets, sun, moon, and certain fixed stars, and the coordinates of the points of intersection of major circles in the celestial sphere, which enabled astronomers and astrologers to make their astronomical calculations and predictions. The term is derived from the Middle Persian word zīk or zīg, meaning cord.
The first zījs produced in the Islamic period were based on the Indo-Persian tradition: Zīj al-Arkand was written in Arabic in the year 735 based on Indian tables; Zīj-i Shahriyār was translated from Pahlavi in the final years of the 8th century (Muslim astronomers knew it in the Pahlavi original long before its translation); and Zīj al-Sindhind was translated from Sanskrit in the 770s by al-Fazārī and Ya‘qūb ibn Tāriq, the court scholars of the ‘Abbasid caliph al-Mansūr. However, in the first half of the 9th century al-Khwārizmī, a Persian mathematician and astronomer who lived in Baghdad, compiled a zīj, which is the first extant original Islamic astronomical table. Although elements from the previously translated tables are used in this zīj, Ptolemaic elements were also introduced. The zīj was written under the patronage of caliph al-Ma‘mūn, during whose reign (813-33) Ptolemy’s Almagest was twice translated into Arabic.
Mixing parameters from the Indian-Iranian and Ptolemaic tables, as was done in al-Khwārizmī’s zīj and other similar tables, would have created disparities both in practical and predictive astronomy. On the other hand, more than six centuries had elapsed since the time of Ptolemy, during which period the parameters of positional astronomy had altered anyway, so the early Islamic observational astronomers’ struggle with the observational discrepancies was inevitable anyway. The earliest efforts at observational astronomy included attempts to build instruments based on information from Ptolemy and other sources, and to measure some of the basic parameters of positional astronomy such as the obliquity of the ecliptic, the length of the solar year and the length of a degree of latitude, as well as certain lunar parameters. Muslim astronomers also performed observations to fix local coordinates in order to determine the qibla—the sacred direction of Mecca—towards which Muslims face when praying. Through these observational programs, astronomers were able to correct errors found in the ancient observations, and to obtain updated values for astronomical parameters. This helped them avoid using contradictory parameters from different sources.
During al-Ma‘mūn’s reign, other observational programs started in Baghdad and Damascus. New parameters were calculated for the solar, lunar, and planetary motions; the obliquity of the ecliptic was measured; and observations took place to determine the positions of stars. Astronomers also performed geodesic measurements to determine the size of the earth by measuring the length of a degree of latitude (in order to provide a new map of the world), and fixed local coordinates by simultaneous observations of a lunar eclipse from Baghdad and Mecca, in order to determine the qibla in Baghdad. The outcome of these diverse observations was (directly or indirectly) influential in providing new zījs, among them al-Zīj al-Mumtahan and the zīj of Habash al-Hāsib. In these tables, not only were new values used for astronomical parameters; new computational techniques were also employed, as one can see from the use of new spherical trigonometry in the zīj of Habash al-Hāsib. In addition, the comparison of the results of these observations with those from the Hellenistic period led to important corrections to the existing kinematic models. For instance, it was established that, contra Ptolemy and Hipparchus, the position of the solar apogee with respect to the vernal equinox was not fixed.
This observational tradition persisted after al-Ma‘mūn. Among the astronomers of the second half of the 9th century was Thābit ibn Qurra (836-901), a polymath and the editor of an Arabic translation of Ptolemy’s Almagest. Thābit was a Sābian from Harran (now in southern Turkey). Sābians were the followers of an ancient religious order who worshipped the heavenly bodies. Thābit carefully observed the motions of the sun and the moon, measured the length of the sidereal year, determined the solar apogee and eccentricity, and wrote the Book on the Solar Year, On the Visibility of the New Moon, and a book concerning the apparent motion of the moon based on Ptolemy’s lunar theory. Thābit also concluded that the precession of the equinoxes was not linear, but rather that it was oscillating periodically. He explained this theory of the trepidation of the equinoxes in his treatise On the Motion of the Eighth Sphere. Thābit proposed that the poles of the eighth sphere were moving on small circles whose centres held the poles of a ninth sphere.
A contemporary of Thābit, the astronomer al-Battānī or Albategnius in its Latinized form (c. 850-929), observing from a city located on the north bank of the Euphrates, calculated a new figure for the obliquity of the ecliptic (23° 35′ instead of Ptolemy’s 23° 51′ 20″), found an accurate value for the eccentricity of the sun (0.017326 instead of Ptolemy’s 0.0175), observed the planetary motions carefully, and improved the observed values for the moon’s mean motion in longitude. In his zīj (known as al-zīj al-Sābi‘ī) al-Battānī not only used improved values for most of the planetary parameters, but also employed new formulae in spherical trigonometry. In addition, he introduced revised or new types of observational instruments, such as a new sundial, an armillary, and a mural quadrant. Al-Battānī, for the first time in the history of astronomy, talked about the possibility of solar annular eclipses, which he deduced from the variations in the apparent sizes of the moon and the sun.
By the beginning of the 11th century, attempts to perform accurate observations, hand in hand with the development of new methods in mathematical astronomy, became a characteristic feature of Islamic astronomy: the astronomers concerned include ‘Abd al-Rahmān al-Sūfī (903-86), Abū‘l Wafā al-Būzjānī (d. c. 997), Ibn Yūnus (d. 1009), and Abū Rayhān al-Bīrūnī (973-1048). The Persian al-Sūfī, in his Book of Fixed Stars (964)—which was the first complete survey of the night sky since Ptolemy—provided an accurate star catalogue with corrections to the positional data and magnitudes in Ptolemy’s star list. He also described a number of nebulous objects which we now categorize as galaxies and star clusters. Abū‘l Wafā, another Persian astronomer and mathematician, worked mostly on mathematical astronomy and made significant developments in spherical astronomy. By introducing new methods, Abū‘l Wafā made the solution of problems involving oblique spherical triangles simpler and more accurate than using Ptolemy’s methods, which were based on the Theorem of Menelaus. Ibn Yūnus, observing in Cairo, prepared an excellent zīj (called the Hakīmī Zīj) which differed from other extant zījs by exhibiting the author’s knowledge of his predecessors’ observations and his awareness of observational errors and computational precision. His tables for timekeeping were still being used in Cairo in the 19th century. The multi-disciplinary scholar al-Bīrūnī not only introduced a sophisticated spherical trigonometry to solve astronomical and geodesic problems, but also attempted to re-measure some of the astronomical parameters and local coordinates.
Meticulous observations such as these became an integral part of astronomy in the Muslim world throughout the following centuries. However, this was not the main contribution of Islamic astronomy. Major developments also occurred in the fields of theoretical and mathematical astronomy. Some of these developments were triggered by practical needs relating to astronomical and geodesic problems in Islamic rituals, while others were theoretical and philosophical in nature. In both aspects, astronomers in the Islamic territories made significant progress in the history of astronomy.

Fig. 1. A page from al-Sūfī’s star catalogue: the constellation Sagittarius as seen on a celestial globe. From ‘Abd al-Rahmān al-Sūfī (Azophi) (964), Book of Fixed Stars. Creative Commons Licence

Fig. 2. Zīj Gurgani [Zīj-i Jurjānī = Gurgani Astronomical Tables]. 1193 H/1779. Beinecke Rare Book & Manuscript Library. (Public domain)
- InfoVersion: 2
Status: PUB
Date: 2012-04-13 21:40:04
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Practical astronomy
The astronomical and geodesic issues relating to Islamic rituals can be discussed under three headings: problems related to timekeeping; the determination of the sacred direction (qibla); and the regulation of the lunar calendar. The exact times of the five daily prayers are based on the position of the sun in the sky: the times of the daylight prayers are determined by the length of shadows, while the times of prayers when the sun is not above the local horizon are established on the basis of twilight phenomena. The morning prayer begins at dawn and ends before sunrise; the noon prayer starts at noon, after the sun crosses the local meridian and the shadow of a vertical object reaches its minimum; the next prayer starts in the afternoon, when the length of the shadow of any object is equal to the sum of its midday minimum shadow and the length of the object casting the shadow; the next prayer starts after the afternoon prayer and ends before sunset; and the final prayer starts when the afterglow disappears and should end before midnight. Although it is not difficult to estimate these prayer times empirically, to determine them accurately one needs to acquire a good knowledge of the local coordinate system and the day-to-day changes in the apparent position of the sun in the sky.
During the first thirteen years of the rise of Islam, Muslims faced Jerusalem while praying. However, seventeen months after the Hijra—the migration of the prophet Muhammad from Mecca to Medina—the orientation of prayers (qibla) changed so as to be towards the Kaaba in Mecca. Since Mecca is located south of Medina, finding the qibla in Medina was not difficult. However, once the Islamic territories expanded, finding the right qibla became a challenging problem in spherical geometry. The problem was to find the direction of the great circle passing through two points on the globe. Over the centuries, Muslim astronomers and mathematicians developed methods to solve this problem based on spherical trigonometry, and produced tables and even sophisticated instruments to find the orientation of Mecca from different locations.
The regulation of the lunar calendar was one of the most important and at the same time one of the most difficult problems for Muslim astronomers. In Islamic sacred law, the lunar month starts with the first sighting of the new crescent moon. Depending on the time that has elapsed since new moon, this first crescent can be very tricky to observe, owing to the short time it stays above the horizon and its faint glow compared to the brightness of the western horizon after sunset. Therefore, one needs to know exactly when and where to look to find the first crescent. Traditionally, observers were sent to locations with an open horizon to report on the visibility of the moon. If they failed to see it, they would need to repeat their observations the next evening. If the horizon was cloudy, fixed number of days had to be assumed for the month in question. These uncertainties, especially for the holy month of Ramadan, were problematic. Early Muslim astronomers, based on Indian sources, developed procedures to define the visibility of the new crescent by calculating the relative distances of the sun and the moon and working out the difference in their setting times. However, in the centuries that followed they developed more complex procedures, taking into account also the angular separation of the sun and the moon and the apparent velocity of the moon, and provided complicated tables to determine the visibility.
- InfoVersion: 8
Status: PUB
Date: 2012-04-13 22:05:54
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Observatories
In order to obtain accurate celestial data for both astronomical and astrological purposes, continuous observational programs were a necessity. While some data can be obtained in a relatively short time with portable instruments, most of the data needed in positional astronomy require long-term observations. As a result, the establishment of observatories became an integral part of astronomical programmes in the Islamic period. According to available sources, the first observatories in Islam were established in Baghdad and Damascus under the patronage of the ‘Abbasid caliph al-Ma‘mūn in the early 9th century. These observatories, which have not survived, were mainly established so as to update the values of astronomical and geodesic parameters in order to compile new zījs, to prepare accurate tables for timekeeping and calendar regulation, and to produce new star maps.
Some scholars made observations independently of al-Ma‘mūn’s observatories, using their own private observational stations. For example, al-Battānī observed for many years in Raqqa (in northern Syria); the Banū Mūsā brothers observed for about thirty years from their own properties in Baghdad and the nearby city of Samarra; the Banū Amājūr family, including the father, two sons, and a freed slave, observed over a long period and made their own zījs; and Sharf al-Dawla built an observatory in the garden of his palace in Baghdad.
From the mid-10th to the mid-13th century, observatories or observational stations were built all over the Islamic territories, with various observational instruments and to perform different astronomical programs. In the 950s al-Sūfī conducted observations in Rayy (near Tehran) and Shiraz; in the late 10th century Abū‘l Wafā al-Būzjānī observed from Baghdad, and observed a lunar eclipse simultaneously with al-Bīrūnī while the latter was in Khwarizm (in modern Turkmenistan); in 994 al-Khujandī measured the obliquity of the ecliptic in Rayy using a sextant about 20m in radius; in the 970s Ibn Yūnus started an extended observational program in Cairo which he explains in his zīj; in the late 10th century and the first two decades of the 11th century al-Bīrūnī conducted observations for more than thirty years in Khurasan (eastern Iran); in the late 11th century ‘Umar al-Khayyām used an observatory in Isfahan, Iran, for about 18 years where he prepared a zīj and supervised the calendar reform project for the Seljuk ruler, Malik Shāh; and finally Sā ‘id al-Andalusī and Ibn al-Zarqāllu undertook a long-term observational program in Spain in the 11th century.
However, two observatories in the Islamic period occupy a special place in the history of astronomy: the Maragha Observatory, built in 1259 in northern Iran under the patronage of Hūlāgū (a grandson of the Mongol conqueror Genghis Khan); and the Samarqand Observatory, founded by Ulugh Beg (a grandson of Tamerlane) in 1424. The scale of the observational instruments in these two observatories, the importance of their observational programmes, their institutional setting, and the number of affiliated astronomers and mathematicians, combine to make these two institutions unique in the history of medieval astronomy.
The Samarqand observatory, which was based upon ideas from the Maragha Observatory, in turn became a model for an observatory built by Taqī al-Dīn in Istanbul in 1575 and the Jantar Mantar observatories in north India in the 1720s. After the fall of Ulugh Beg’s dynasty in the 1450s, a number of scholars in Ulugh Beg’s circle emigrated to the newly born Ottoman Empire, where they strongly influenced scientific developments. Taqī al-Dīn, the court astronomer of Sultan Murad III (reign 1574-95), established an observatory in Istanbul, something the Turkish Sultans had dreamed of ever since they conquered Constantinople in 1453. About fifteen astronomers helped to build and use the instruments, whose purpose was to produce a new zīj. However, after two years the great comet of 1577 appeared, which Taqī al-Dīn interpreted as a sign that the Turkish army would be victorious against Persia. Although the Persian army was defeated in the war, the Turkish troops also suffered heavy losses. In the same year several dignitaries died within short intervals, and there was also a plague. Referring to these unpredicted horrifying events, the Sultan believed that the comet appeared because of the establishment of the observatory and that it would go away if its cause (the observatory) were removed. As a result, the observatory was demolished at once, before Taqī al-Dīn was able to finalize his zīj.
The Jantar Mantar observatories built by Jai Singh in northern India between 1724 and 1734, although built after the invention of the telescope, continued the Islamic-Persian tradition of monumental observatory building and were greatly inspired by the Samarqand Observatory.
- InfoVersion: 21
Status: PUB
Date: 2017-11-10 06:46:56
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Theoretical astronomy
In addition to observational and computational astronomy, Muslim astronomers had a special interest in creating a clear picture of the universe in its physical sense. It was generally accepted that the earth was located at the centre of the universe, with all celestial bodies moving uniformly around it. Aristotle had argued that the celestial region consisted of a series of concentric spheres (or ‘orbs’) with the earth at the centre. Each of the planets, for example, moved at a constant rate around one of these orbs. However, observational data did not support this picture: all celestial bodies from the sun and the moon to the planets and stars manifested different short-term or secular non-uniform motions. To explain these observations, non-concentric models of planetary motions had been developed in the 3rd and 2nd centuries BC, culminating in Ptolemy’s model of the planetary motions. This preserved the concentric orbs but included other eccentric orbs and epicycles embedded in each orb. According to Ptolemy, the uniform motion of a planet or the centre of an epicycle occurred around a point called the equant which did not coincide with the earth. With this innovation, the observations and the mathematical models of the planetary motions became compatible, but the physical structure of the universe became unclear. The problem was simple: given that the eccentric orbs, epicycles and equant were only mathematical devices to make the planetary motions calculable, what was the true physical configuration of the celestial spheres? Even Ptolemy was not explicit in his treatment of the universe: in the Almagest he merely describes the motions and models mathematically, while in his Planetary Hypothesis he talks about the configuration of the spheres without referring to problematic premises that underlie his mathematical models.
Critiques of Ptolemy started to appear soon after Muslim astronomers became familiar with the Ptolemaic system. Doubts concerning either Ptolemy’s observational data or his description of the cosmos became common in Islam. The main challenge was to create a configuration (hay‘a) of the universe that satisfied both observational and physical principles. The main goal, in other words, was to develop models involving uniform motions around the centre of the universe—the earth—that were compatible with observations.


Fig. 3. Left/Top: Tūsī’s couple. Imagine two spheres internally tangent at one point (C), the diameter of the small sphere being equal to half of the other. If the small sphere uniformly moves twice (2α) as fast as the big sphere but in the opposite direction, the common point D will move back and forth along AB. In other words, the uniform circular motions of the two spheres create a linear motion. By choosing a Tūsī’s couple with the right dimensions and speeds of the two revolving spheres, and attaching it to a given sphere, one can produce the observed non-uniform motion of a particular planet around the central earth, even though the motion of the revolving spheres is uniform. Therefore, both observation and physical principles are preserved. © Tofigh Heidarzadeh. Right/Bottom: Tūsī’s diagram of the couple, showing the oscillation of a given point along the diameter of the big circle. After Tūsī couple from Vat. Arabic ms 319, commons.wikimedia.org. Creative Commons Licence
Solving this problem occupied the minds of several Muslim astronomers, among them Ibn al-Haytham, Ibn-Sīnā’s student Abū ‘Ubeyd Jūzjānī, Ibn Rūshd, and Ibn Bājja. However, it was Nasīr al-Dīn al-Tūsī who developed a revolutionary solution to eliminate the equant. Tūsī introduced an arrangement in which the circular motions of two spheres produced a linear motion displacing a point (for example the centre of an epicycle) closer to or further from a central point. This arrangement (called Tūsī’s couple), which was able to produce non-uniform motions from concentric uniform motions, was a key concept in the development of non-Ptolemaic models. Tūsī’s contemporaries Mu‘ayyad al-Dīn al-‘Urdī and Qutb al-Dīn Shīrazī also developed innovative non-Ptolemaic models, and the tradition continued with further models produced by Alī Al-Qūshjī (of Samarqand Observatory) and Ibn al-Shātir (1304-75), the timekeeper of the Umayyad Mosque in Damascus.
Copernicus repeatedly used concepts developed by Tūsī and his followers and colleagues. In De revolutionibus he employed Tūsī’s couple to create the variation in the obliquity of the ecliptic and to produce an oscillation in the orbital planes of planets. In the Commentariolus Copernicus uses al-‘Urdī and Ibn al-Shātir’s models to develop his own models for planetary longitude. Copernicus’s model for the lunar motions is almost the same as the model proposed by Ibn al-Shātir. Copernicus probably became aware of Muslim non-Ptolemaic models, especially those developed by Tūsī and his followers, when he was studying in Italy, where there was easier access to Arabic texts.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.
- InfoVersion: 15
Status: PUB
Date: 2017-11-09 14:30:06
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Our knowledge about the extent of peoples’ familiarity with astronomy in the Arabian Peninsula in pre-Islamic times is limited. However, it is known that they were familiar with the sun’s journey through the zodiacal signs, and that they adopted a lunar calendar, defined lunar mansions by identifying certain fixed stars and asterisms, and used the rising and setting times of certain specific stars to predict seasonal and meteorological phenomena.
The rapid expansion of the Islamic territories from the mid-7th century onwards put Muslims in contact with Persians and Byzantines who had a long tradition in astronomy. However, Muslims’ acquaintance with ‘foreign’ sciences, including astronomy, really began in the late 8th century when the first translations of Greek, Syriac and Persian works into Arabic became available in the court of the ‘Abbasid caliph, al-Mansūr, in the newly built capital city of Baghdad. The establishment of the House of Wisdom, an institute for research and translation, in the early 9th century in Baghdad led to the start of the great project of translating scientific and philosophical books from the Greek, Hellenistic, Persian, and Indian traditions.
Before long, thanks to the translation of works such as the Persian Zīj-i Shahriyār (translated into Arabic as Zīj al-Shāh), the Sindhind (Indian astronomical tables in Sanskrit), Ptolemy’s Mathematikē Sýntaxis (Mathematical Treatise, commonly called Almagest, based on the Latin form of its Arabic title, Kitab al-Majistī, The Great Book), and other mathematical works from the Greek and Hellenistic traditions, Muslims became familiar with planetary models and mathematical astronomy. However, it was Ptolemaic astronomy that finally became dominant among Muslim astronomers, although preparing zījs based on the Indo-Persian tradition also continued. During the 8th and 9th centuries, Ptolemy’s Almagest was translated at least five times into Arabic, and his other works—most importantly the Planetary Hypothesis—also became known to astronomers practising in the Islamic territories. When the main texts became available, several commentaries, critical revisions, and summaries also appeared. Some of these discussed the difficulties and inconsistencies found in the original texts, while others helped to make them comprehensible to students.
Muslims’ first introduction to computational astronomy was through the zījs. A zīj is a combination of tables consisting of observational data about the motion and position of the planets, sun, moon, and certain fixed stars, and the coordinates of the points of intersection of major circles in the celestial sphere, which enabled astronomers and astrologers to make their astronomical calculations and predictions. The term is derived from the Middle Persian word zīk or zīg, meaning cord.
The first zījs produced in the Islamic period were based on the Indo-Persian tradition: Zīj al-Arkand was written in Arabic in the year 735 based on Indian tables; Zīj-i Shahriyār was translated from Pahlavi in the final years of the 8th century (Muslim astronomers knew it in the Pahlavi original long before its translation); and Zīj al-Sindhind was translated from Sanskrit in the 770s by al-Fazārī and Ya‘qūb ibn Tāriq, the court scholars of the ‘Abbasid caliph al-Mansūr. However, in the first half of the 9th century al-Khwārizmī, a Persian mathematician and astronomer who lived in Baghdad, compiled a zīj, which is the first extant original Islamic astronomical table. Although elements from the previously translated tables are used in this zīj, Ptolemaic elements were also introduced. The zīj was written under the patronage of caliph al-Ma‘mūn, during whose reign (813-33) Ptolemy’s Almagest was twice translated into Arabic.
Mixing parameters from the Indian-Iranian and Ptolemaic tables, as was done in al-Khwārizmī’s zīj and other similar tables, would have created disparities both in practical and predictive astronomy. On the other hand, more than six centuries had elapsed since the time of Ptolemy, during which period the parameters of positional astronomy had altered anyway, so the early Islamic observational astronomers’ struggle with the observational discrepancies was inevitable anyway. The earliest efforts at observational astronomy included attempts to build instruments based on information from Ptolemy and other sources, and to measure some of the basic parameters of positional astronomy such as the obliquity of the ecliptic, the length of the solar year and the length of a degree of latitude, as well as certain lunar parameters. Muslim astronomers also performed observations to fix local coordinates in order to determine the qibla—the sacred direction of Mecca—towards which Muslims face when praying. Through these observational programs, astronomers were able to correct errors found in the ancient observations, and to obtain updated values for astronomical parameters. This helped them avoid using contradictory parameters from different sources.
During al-Ma‘mūn’s reign, other observational programs started in Baghdad and Damascus. New parameters were calculated for the solar, lunar, and planetary motions; the obliquity of the ecliptic was measured; and observations took place to determine the positions of stars. Astronomers also performed geodesic measurements to determine the size of the earth by measuring the length of a degree of latitude (in order to provide a new map of the world), and fixed local coordinates by simultaneous observations of a lunar eclipse from Baghdad and Mecca, in order to determine the qibla in Baghdad. The outcome of these diverse observations was (directly or indirectly) influential in providing new zījs, among them al-Zīj al-Mumtahan and the zīj of Habash al-Hāsib. In these tables, not only were new values used for astronomical parameters; new computational techniques were also employed, as one can see from the use of new spherical trigonometry in the zīj of Habash al-Hāsib. In addition, the comparison of the results of these observations with those from the Hellenistic period led to important corrections to the existing kinematic models. For instance, it was established that, contra Ptolemy and Hipparchus, the position of the solar apogee with respect to the vernal equinox was not fixed.
This observational tradition persisted after al-Ma‘mūn. Among the astronomers of the second half of the 9th century was Thābit ibn Qurra (836-901), a polymath and the editor of an Arabic translation of Ptolemy’s Almagest. Thābit was a Sābian from Harran (now in southern Turkey). Sābians were the followers of an ancient religious order who worshipped the heavenly bodies. Thābit carefully observed the motions of the sun and the moon, measured the length of the sidereal year, determined the solar apogee and eccentricity, and wrote the Book on the Solar Year, On the Visibility of the New Moon, and a book concerning the apparent motion of the moon based on Ptolemy’s lunar theory. Thābit also concluded that the precession of the equinoxes was not linear, but rather that it was oscillating periodically. He explained this theory of the trepidation of the equinoxes in his treatise On the Motion of the Eighth Sphere. Thābit proposed that the poles of the eighth sphere were moving on small circles whose centres held the poles of a ninth sphere.
A contemporary of Thābit, the astronomer al-Battānī or Albategnius in its Latinized form (c. 850-929), observing from a city located on the north bank of the Euphrates, calculated a new figure for the obliquity of the ecliptic (23° 35′ instead of Ptolemy’s 23° 51′ 20″), found an accurate value for the eccentricity of the sun (0.017326 instead of Ptolemy’s 0.0175), observed the planetary motions carefully, and improved the observed values for the moon’s mean motion in longitude. In his zīj (known as al-zīj al-Sābi‘ī) al-Battānī not only used improved values for most of the planetary parameters, but also employed new formulae in spherical trigonometry. In addition, he introduced revised or new types of observational instruments, such as a new sundial, an armillary, and a mural quadrant. Al-Battānī, for the first time in the history of astronomy, talked about the possibility of solar annular eclipses, which he deduced from the variations in the apparent sizes of the moon and the sun.
By the beginning of the 11th century, attempts to perform accurate observations, hand in hand with the development of new methods in mathematical astronomy, became a characteristic feature of Islamic astronomy: the astronomers concerned include ‘Abd al-Rahmān al-Sūfī (903-86), Abū‘l Wafā al-Būzjānī (d. c. 997), Ibn Yūnus (d. 1009), and Abū Rayhān al-Bīrūnī (973-1048). The Persian al-Sūfī, in his Book of Fixed Stars (964)—which was the first complete survey of the night sky since Ptolemy—provided an accurate star catalogue with corrections to the positional data and magnitudes in Ptolemy’s star list. He also described a number of nebulous objects which we now categorize as galaxies and star clusters. Abū‘l Wafā, another Persian astronomer and mathematician, worked mostly on mathematical astronomy and made significant developments in spherical astronomy. By introducing new methods, Abū‘l Wafā made the solution of problems involving oblique spherical triangles simpler and more accurate than using Ptolemy’s methods, which were based on the Theorem of Menelaus. Ibn Yūnus, observing in Cairo, prepared an excellent zīj (called the Hakīmī Zīj) which differed from other extant zījs by exhibiting the author’s knowledge of his predecessors’ observations and his awareness of observational errors and computational precision. His tables for timekeeping were still being used in Cairo in the 19th century. The multi-disciplinary scholar al-Bīrūnī not only introduced a sophisticated spherical trigonometry to solve astronomical and geodesic problems, but also attempted to re-measure some of the astronomical parameters and local coordinates.
Meticulous observations such as these became an integral part of astronomy in the Muslim world throughout the following centuries. However, this was not the main contribution of Islamic astronomy. Major developments also occurred in the fields of theoretical and mathematical astronomy. Some of these developments were triggered by practical needs relating to astronomical and geodesic problems in Islamic rituals, while others were theoretical and philosophical in nature. In both aspects, astronomers in the Islamic territories made significant progress in the history of astronomy.

Fig. 1. A page from al-Sūfī’s star catalogue: the constellation Sagittarius as seen on a celestial globe. From ‘Abd al-Rahmān al-Sūfī (Azophi) (964), Book of Fixed Stars. Creative Commons Licence

Fig. 2. Zīj Gurgani [Zīj-i Jurjānī = Gurgani Astronomical Tables]. 1193 H/1779. Beinecke Rare Book & Manuscript Library. (Public domain)
- InfoVersion: 2
Status: PUB
Date: 2012-04-13 21:40:04
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Practical astronomy
The astronomical and geodesic issues relating to Islamic rituals can be discussed under three headings: problems related to timekeeping; the determination of the sacred direction (qibla); and the regulation of the lunar calendar. The exact times of the five daily prayers are based on the position of the sun in the sky: the times of the daylight prayers are determined by the length of shadows, while the times of prayers when the sun is not above the local horizon are established on the basis of twilight phenomena. The morning prayer begins at dawn and ends before sunrise; the noon prayer starts at noon, after the sun crosses the local meridian and the shadow of a vertical object reaches its minimum; the next prayer starts in the afternoon, when the length of the shadow of any object is equal to the sum of its midday minimum shadow and the length of the object casting the shadow; the next prayer starts after the afternoon prayer and ends before sunset; and the final prayer starts when the afterglow disappears and should end before midnight. Although it is not difficult to estimate these prayer times empirically, to determine them accurately one needs to acquire a good knowledge of the local coordinate system and the day-to-day changes in the apparent position of the sun in the sky.
During the first thirteen years of the rise of Islam, Muslims faced Jerusalem while praying. However, seventeen months after the Hijra—the migration of the prophet Muhammad from Mecca to Medina—the orientation of prayers (qibla) changed so as to be towards the Kaaba in Mecca. Since Mecca is located south of Medina, finding the qibla in Medina was not difficult. However, once the Islamic territories expanded, finding the right qibla became a challenging problem in spherical geometry. The problem was to find the direction of the great circle passing through two points on the globe. Over the centuries, Muslim astronomers and mathematicians developed methods to solve this problem based on spherical trigonometry, and produced tables and even sophisticated instruments to find the orientation of Mecca from different locations.
The regulation of the lunar calendar was one of the most important and at the same time one of the most difficult problems for Muslim astronomers. In Islamic sacred law, the lunar month starts with the first sighting of the new crescent moon. Depending on the time that has elapsed since new moon, this first crescent can be very tricky to observe, owing to the short time it stays above the horizon and its faint glow compared to the brightness of the western horizon after sunset. Therefore, one needs to know exactly when and where to look to find the first crescent. Traditionally, observers were sent to locations with an open horizon to report on the visibility of the moon. If they failed to see it, they would need to repeat their observations the next evening. If the horizon was cloudy, fixed number of days had to be assumed for the month in question. These uncertainties, especially for the holy month of Ramadan, were problematic. Early Muslim astronomers, based on Indian sources, developed procedures to define the visibility of the new crescent by calculating the relative distances of the sun and the moon and working out the difference in their setting times. However, in the centuries that followed they developed more complex procedures, taking into account also the angular separation of the sun and the moon and the apparent velocity of the moon, and provided complicated tables to determine the visibility.
- InfoVersion: 8
Status: PUB
Date: 2012-04-13 22:05:54
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Observatories
In order to obtain accurate celestial data for both astronomical and astrological purposes, continuous observational programs were a necessity. While some data can be obtained in a relatively short time with portable instruments, most of the data needed in positional astronomy require long-term observations. As a result, the establishment of observatories became an integral part of astronomical programmes in the Islamic period. According to available sources, the first observatories in Islam were established in Baghdad and Damascus under the patronage of the ‘Abbasid caliph al-Ma‘mūn in the early 9th century. These observatories, which have not survived, were mainly established so as to update the values of astronomical and geodesic parameters in order to compile new zījs, to prepare accurate tables for timekeeping and calendar regulation, and to produce new star maps.
Some scholars made observations independently of al-Ma‘mūn’s observatories, using their own private observational stations. For example, al-Battānī observed for many years in Raqqa (in northern Syria); the Banū Mūsā brothers observed for about thirty years from their own properties in Baghdad and the nearby city of Samarra; the Banū Amājūr family, including the father, two sons, and a freed slave, observed over a long period and made their own zījs; and Sharf al-Dawla built an observatory in the garden of his palace in Baghdad.
From the mid-10th to the mid-13th century, observatories or observational stations were built all over the Islamic territories, with various observational instruments and to perform different astronomical programs. In the 950s al-Sūfī conducted observations in Rayy (near Tehran) and Shiraz; in the late 10th century Abū‘l Wafā al-Būzjānī observed from Baghdad, and observed a lunar eclipse simultaneously with al-Bīrūnī while the latter was in Khwarizm (in modern Turkmenistan); in 994 al-Khujandī measured the obliquity of the ecliptic in Rayy using a sextant about 20m in radius; in the 970s Ibn Yūnus started an extended observational program in Cairo which he explains in his zīj; in the late 10th century and the first two decades of the 11th century al-Bīrūnī conducted observations for more than thirty years in Khurasan (eastern Iran); in the late 11th century ‘Umar al-Khayyām used an observatory in Isfahan, Iran, for about 18 years where he prepared a zīj and supervised the calendar reform project for the Seljuk ruler, Malik Shāh; and finally Sā ‘id al-Andalusī and Ibn al-Zarqāllu undertook a long-term observational program in Spain in the 11th century.
However, two observatories in the Islamic period occupy a special place in the history of astronomy: the Maragha Observatory, built in 1259 in northern Iran under the patronage of Hūlāgū (a grandson of the Mongol conqueror Genghis Khan); and the Samarqand Observatory, founded by Ulugh Beg (a grandson of Tamerlane) in 1424. The scale of the observational instruments in these two observatories, the importance of their observational programmes, their institutional setting, and the number of affiliated astronomers and mathematicians, combine to make these two institutions unique in the history of medieval astronomy.
The Samarqand observatory, which was based upon ideas from the Maragha Observatory, in turn became a model for an observatory built by Taqī al-Dīn in Istanbul in 1575 and the Jantar Mantar observatories in north India in the 1720s. After the fall of Ulugh Beg’s dynasty in the 1450s, a number of scholars in Ulugh Beg’s circle emigrated to the newly born Ottoman Empire, where they strongly influenced scientific developments. Taqī al-Dīn, the court astronomer of Sultan Murad III (reign 1574-95), established an observatory in Istanbul, something the Turkish Sultans had dreamed of ever since they conquered Constantinople in 1453. About fifteen astronomers helped to build and use the instruments, whose purpose was to produce a new zīj. However, after two years the great comet of 1577 appeared, which Taqī al-Dīn interpreted as a sign that the Turkish army would be victorious against Persia. Although the Persian army was defeated in the war, the Turkish troops also suffered heavy losses. In the same year several dignitaries died within short intervals, and there was also a plague. Referring to these unpredicted horrifying events, the Sultan believed that the comet appeared because of the establishment of the observatory and that it would go away if its cause (the observatory) were removed. As a result, the observatory was demolished at once, before Taqī al-Dīn was able to finalize his zīj.
The Jantar Mantar observatories built by Jai Singh in northern India between 1724 and 1734, although built after the invention of the telescope, continued the Islamic-Persian tradition of monumental observatory building and were greatly inspired by the Samarqand Observatory.
- InfoVersion: 21
Status: PUB
Date: 2017-11-10 06:46:56
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Theoretical astronomy
In addition to observational and computational astronomy, Muslim astronomers had a special interest in creating a clear picture of the universe in its physical sense. It was generally accepted that the earth was located at the centre of the universe, with all celestial bodies moving uniformly around it. Aristotle had argued that the celestial region consisted of a series of concentric spheres (or ‘orbs’) with the earth at the centre. Each of the planets, for example, moved at a constant rate around one of these orbs. However, observational data did not support this picture: all celestial bodies from the sun and the moon to the planets and stars manifested different short-term or secular non-uniform motions. To explain these observations, non-concentric models of planetary motions had been developed in the 3rd and 2nd centuries BC, culminating in Ptolemy’s model of the planetary motions. This preserved the concentric orbs but included other eccentric orbs and epicycles embedded in each orb. According to Ptolemy, the uniform motion of a planet or the centre of an epicycle occurred around a point called the equant which did not coincide with the earth. With this innovation, the observations and the mathematical models of the planetary motions became compatible, but the physical structure of the universe became unclear. The problem was simple: given that the eccentric orbs, epicycles and equant were only mathematical devices to make the planetary motions calculable, what was the true physical configuration of the celestial spheres? Even Ptolemy was not explicit in his treatment of the universe: in the Almagest he merely describes the motions and models mathematically, while in his Planetary Hypothesis he talks about the configuration of the spheres without referring to problematic premises that underlie his mathematical models.
Critiques of Ptolemy started to appear soon after Muslim astronomers became familiar with the Ptolemaic system. Doubts concerning either Ptolemy’s observational data or his description of the cosmos became common in Islam. The main challenge was to create a configuration (hay‘a) of the universe that satisfied both observational and physical principles. The main goal, in other words, was to develop models involving uniform motions around the centre of the universe—the earth—that were compatible with observations.


Fig. 3. Left/Top: Tūsī’s couple. Imagine two spheres internally tangent at one point (C), the diameter of the small sphere being equal to half of the other. If the small sphere uniformly moves twice (2α) as fast as the big sphere but in the opposite direction, the common point D will move back and forth along AB. In other words, the uniform circular motions of the two spheres create a linear motion. By choosing a Tūsī’s couple with the right dimensions and speeds of the two revolving spheres, and attaching it to a given sphere, one can produce the observed non-uniform motion of a particular planet around the central earth, even though the motion of the revolving spheres is uniform. Therefore, both observation and physical principles are preserved. © Tofigh Heidarzadeh. Right/Bottom: Tūsī’s diagram of the couple, showing the oscillation of a given point along the diameter of the big circle. After Tūsī couple from Vat. Arabic ms 319, commons.wikimedia.org. Creative Commons Licence
Solving this problem occupied the minds of several Muslim astronomers, among them Ibn al-Haytham, Ibn-Sīnā’s student Abū ‘Ubeyd Jūzjānī, Ibn Rūshd, and Ibn Bājja. However, it was Nasīr al-Dīn al-Tūsī who developed a revolutionary solution to eliminate the equant. Tūsī introduced an arrangement in which the circular motions of two spheres produced a linear motion displacing a point (for example the centre of an epicycle) closer to or further from a central point. This arrangement (called Tūsī’s couple), which was able to produce non-uniform motions from concentric uniform motions, was a key concept in the development of non-Ptolemaic models. Tūsī’s contemporaries Mu‘ayyad al-Dīn al-‘Urdī and Qutb al-Dīn Shīrazī also developed innovative non-Ptolemaic models, and the tradition continued with further models produced by Alī Al-Qūshjī (of Samarqand Observatory) and Ibn al-Shātir (1304-75), the timekeeper of the Umayyad Mosque in Damascus.
Copernicus repeatedly used concepts developed by Tūsī and his followers and colleagues. In De revolutionibus he employed Tūsī’s couple to create the variation in the obliquity of the ecliptic and to produce an oscillation in the orbital planes of planets. In the Commentariolus Copernicus uses al-‘Urdī and Ibn al-Shātir’s models to develop his own models for planetary longitude. Copernicus’s model for the lunar motions is almost the same as the model proposed by Ibn al-Shātir. Copernicus probably became aware of Muslim non-Ptolemaic models, especially those developed by Tūsī and his followers, when he was studying in Italy, where there was easier access to Arabic texts.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.
- InfoVersion: 2
Status: PUB
Date: 2012-04-13 21:40:04
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Practical astronomy
The astronomical and geodesic issues relating to Islamic rituals can be discussed under three headings: problems related to timekeeping; the determination of the sacred direction (qibla); and the regulation of the lunar calendar. The exact times of the five daily prayers are based on the position of the sun in the sky: the times of the daylight prayers are determined by the length of shadows, while the times of prayers when the sun is not above the local horizon are established on the basis of twilight phenomena. The morning prayer begins at dawn and ends before sunrise; the noon prayer starts at noon, after the sun crosses the local meridian and the shadow of a vertical object reaches its minimum; the next prayer starts in the afternoon, when the length of the shadow of any object is equal to the sum of its midday minimum shadow and the length of the object casting the shadow; the next prayer starts after the afternoon prayer and ends before sunset; and the final prayer starts when the afterglow disappears and should end before midnight. Although it is not difficult to estimate these prayer times empirically, to determine them accurately one needs to acquire a good knowledge of the local coordinate system and the day-to-day changes in the apparent position of the sun in the sky.
During the first thirteen years of the rise of Islam, Muslims faced Jerusalem while praying. However, seventeen months after the Hijra—the migration of the prophet Muhammad from Mecca to Medina—the orientation of prayers (qibla) changed so as to be towards the Kaaba in Mecca. Since Mecca is located south of Medina, finding the qibla in Medina was not difficult. However, once the Islamic territories expanded, finding the right qibla became a challenging problem in spherical geometry. The problem was to find the direction of the great circle passing through two points on the globe. Over the centuries, Muslim astronomers and mathematicians developed methods to solve this problem based on spherical trigonometry, and produced tables and even sophisticated instruments to find the orientation of Mecca from different locations.
The regulation of the lunar calendar was one of the most important and at the same time one of the most difficult problems for Muslim astronomers. In Islamic sacred law, the lunar month starts with the first sighting of the new crescent moon. Depending on the time that has elapsed since new moon, this first crescent can be very tricky to observe, owing to the short time it stays above the horizon and its faint glow compared to the brightness of the western horizon after sunset. Therefore, one needs to know exactly when and where to look to find the first crescent. Traditionally, observers were sent to locations with an open horizon to report on the visibility of the moon. If they failed to see it, they would need to repeat their observations the next evening. If the horizon was cloudy, fixed number of days had to be assumed for the month in question. These uncertainties, especially for the holy month of Ramadan, were problematic. Early Muslim astronomers, based on Indian sources, developed procedures to define the visibility of the new crescent by calculating the relative distances of the sun and the moon and working out the difference in their setting times. However, in the centuries that followed they developed more complex procedures, taking into account also the angular separation of the sun and the moon and the apparent velocity of the moon, and provided complicated tables to determine the visibility.
- InfoVersion: 8
Status: PUB
Date: 2012-04-13 22:05:54
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Observatories
In order to obtain accurate celestial data for both astronomical and astrological purposes, continuous observational programs were a necessity. While some data can be obtained in a relatively short time with portable instruments, most of the data needed in positional astronomy require long-term observations. As a result, the establishment of observatories became an integral part of astronomical programmes in the Islamic period. According to available sources, the first observatories in Islam were established in Baghdad and Damascus under the patronage of the ‘Abbasid caliph al-Ma‘mūn in the early 9th century. These observatories, which have not survived, were mainly established so as to update the values of astronomical and geodesic parameters in order to compile new zījs, to prepare accurate tables for timekeeping and calendar regulation, and to produce new star maps.
Some scholars made observations independently of al-Ma‘mūn’s observatories, using their own private observational stations. For example, al-Battānī observed for many years in Raqqa (in northern Syria); the Banū Mūsā brothers observed for about thirty years from their own properties in Baghdad and the nearby city of Samarra; the Banū Amājūr family, including the father, two sons, and a freed slave, observed over a long period and made their own zījs; and Sharf al-Dawla built an observatory in the garden of his palace in Baghdad.
From the mid-10th to the mid-13th century, observatories or observational stations were built all over the Islamic territories, with various observational instruments and to perform different astronomical programs. In the 950s al-Sūfī conducted observations in Rayy (near Tehran) and Shiraz; in the late 10th century Abū‘l Wafā al-Būzjānī observed from Baghdad, and observed a lunar eclipse simultaneously with al-Bīrūnī while the latter was in Khwarizm (in modern Turkmenistan); in 994 al-Khujandī measured the obliquity of the ecliptic in Rayy using a sextant about 20m in radius; in the 970s Ibn Yūnus started an extended observational program in Cairo which he explains in his zīj; in the late 10th century and the first two decades of the 11th century al-Bīrūnī conducted observations for more than thirty years in Khurasan (eastern Iran); in the late 11th century ‘Umar al-Khayyām used an observatory in Isfahan, Iran, for about 18 years where he prepared a zīj and supervised the calendar reform project for the Seljuk ruler, Malik Shāh; and finally Sā ‘id al-Andalusī and Ibn al-Zarqāllu undertook a long-term observational program in Spain in the 11th century.
However, two observatories in the Islamic period occupy a special place in the history of astronomy: the Maragha Observatory, built in 1259 in northern Iran under the patronage of Hūlāgū (a grandson of the Mongol conqueror Genghis Khan); and the Samarqand Observatory, founded by Ulugh Beg (a grandson of Tamerlane) in 1424. The scale of the observational instruments in these two observatories, the importance of their observational programmes, their institutional setting, and the number of affiliated astronomers and mathematicians, combine to make these two institutions unique in the history of medieval astronomy.
The Samarqand observatory, which was based upon ideas from the Maragha Observatory, in turn became a model for an observatory built by Taqī al-Dīn in Istanbul in 1575 and the Jantar Mantar observatories in north India in the 1720s. After the fall of Ulugh Beg’s dynasty in the 1450s, a number of scholars in Ulugh Beg’s circle emigrated to the newly born Ottoman Empire, where they strongly influenced scientific developments. Taqī al-Dīn, the court astronomer of Sultan Murad III (reign 1574-95), established an observatory in Istanbul, something the Turkish Sultans had dreamed of ever since they conquered Constantinople in 1453. About fifteen astronomers helped to build and use the instruments, whose purpose was to produce a new zīj. However, after two years the great comet of 1577 appeared, which Taqī al-Dīn interpreted as a sign that the Turkish army would be victorious against Persia. Although the Persian army was defeated in the war, the Turkish troops also suffered heavy losses. In the same year several dignitaries died within short intervals, and there was also a plague. Referring to these unpredicted horrifying events, the Sultan believed that the comet appeared because of the establishment of the observatory and that it would go away if its cause (the observatory) were removed. As a result, the observatory was demolished at once, before Taqī al-Dīn was able to finalize his zīj.
The Jantar Mantar observatories built by Jai Singh in northern India between 1724 and 1734, although built after the invention of the telescope, continued the Islamic-Persian tradition of monumental observatory building and were greatly inspired by the Samarqand Observatory.
- InfoVersion: 21
Status: PUB
Date: 2017-11-10 06:46:56
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Theoretical astronomy
In addition to observational and computational astronomy, Muslim astronomers had a special interest in creating a clear picture of the universe in its physical sense. It was generally accepted that the earth was located at the centre of the universe, with all celestial bodies moving uniformly around it. Aristotle had argued that the celestial region consisted of a series of concentric spheres (or ‘orbs’) with the earth at the centre. Each of the planets, for example, moved at a constant rate around one of these orbs. However, observational data did not support this picture: all celestial bodies from the sun and the moon to the planets and stars manifested different short-term or secular non-uniform motions. To explain these observations, non-concentric models of planetary motions had been developed in the 3rd and 2nd centuries BC, culminating in Ptolemy’s model of the planetary motions. This preserved the concentric orbs but included other eccentric orbs and epicycles embedded in each orb. According to Ptolemy, the uniform motion of a planet or the centre of an epicycle occurred around a point called the equant which did not coincide with the earth. With this innovation, the observations and the mathematical models of the planetary motions became compatible, but the physical structure of the universe became unclear. The problem was simple: given that the eccentric orbs, epicycles and equant were only mathematical devices to make the planetary motions calculable, what was the true physical configuration of the celestial spheres? Even Ptolemy was not explicit in his treatment of the universe: in the Almagest he merely describes the motions and models mathematically, while in his Planetary Hypothesis he talks about the configuration of the spheres without referring to problematic premises that underlie his mathematical models.
Critiques of Ptolemy started to appear soon after Muslim astronomers became familiar with the Ptolemaic system. Doubts concerning either Ptolemy’s observational data or his description of the cosmos became common in Islam. The main challenge was to create a configuration (hay‘a) of the universe that satisfied both observational and physical principles. The main goal, in other words, was to develop models involving uniform motions around the centre of the universe—the earth—that were compatible with observations.


Fig. 3. Left/Top: Tūsī’s couple. Imagine two spheres internally tangent at one point (C), the diameter of the small sphere being equal to half of the other. If the small sphere uniformly moves twice (2α) as fast as the big sphere but in the opposite direction, the common point D will move back and forth along AB. In other words, the uniform circular motions of the two spheres create a linear motion. By choosing a Tūsī’s couple with the right dimensions and speeds of the two revolving spheres, and attaching it to a given sphere, one can produce the observed non-uniform motion of a particular planet around the central earth, even though the motion of the revolving spheres is uniform. Therefore, both observation and physical principles are preserved. © Tofigh Heidarzadeh. Right/Bottom: Tūsī’s diagram of the couple, showing the oscillation of a given point along the diameter of the big circle. After Tūsī couple from Vat. Arabic ms 319, commons.wikimedia.org. Creative Commons Licence
Solving this problem occupied the minds of several Muslim astronomers, among them Ibn al-Haytham, Ibn-Sīnā’s student Abū ‘Ubeyd Jūzjānī, Ibn Rūshd, and Ibn Bājja. However, it was Nasīr al-Dīn al-Tūsī who developed a revolutionary solution to eliminate the equant. Tūsī introduced an arrangement in which the circular motions of two spheres produced a linear motion displacing a point (for example the centre of an epicycle) closer to or further from a central point. This arrangement (called Tūsī’s couple), which was able to produce non-uniform motions from concentric uniform motions, was a key concept in the development of non-Ptolemaic models. Tūsī’s contemporaries Mu‘ayyad al-Dīn al-‘Urdī and Qutb al-Dīn Shīrazī also developed innovative non-Ptolemaic models, and the tradition continued with further models produced by Alī Al-Qūshjī (of Samarqand Observatory) and Ibn al-Shātir (1304-75), the timekeeper of the Umayyad Mosque in Damascus.
Copernicus repeatedly used concepts developed by Tūsī and his followers and colleagues. In De revolutionibus he employed Tūsī’s couple to create the variation in the obliquity of the ecliptic and to produce an oscillation in the orbital planes of planets. In the Commentariolus Copernicus uses al-‘Urdī and Ibn al-Shātir’s models to develop his own models for planetary longitude. Copernicus’s model for the lunar motions is almost the same as the model proposed by Ibn al-Shātir. Copernicus probably became aware of Muslim non-Ptolemaic models, especially those developed by Tūsī and his followers, when he was studying in Italy, where there was easier access to Arabic texts.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.
- InfoVersion: 8
Status: PUB
Date: 2012-04-13 22:05:54
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Observatories
In order to obtain accurate celestial data for both astronomical and astrological purposes, continuous observational programs were a necessity. While some data can be obtained in a relatively short time with portable instruments, most of the data needed in positional astronomy require long-term observations. As a result, the establishment of observatories became an integral part of astronomical programmes in the Islamic period. According to available sources, the first observatories in Islam were established in Baghdad and Damascus under the patronage of the ‘Abbasid caliph al-Ma‘mūn in the early 9th century. These observatories, which have not survived, were mainly established so as to update the values of astronomical and geodesic parameters in order to compile new zījs, to prepare accurate tables for timekeeping and calendar regulation, and to produce new star maps.
Some scholars made observations independently of al-Ma‘mūn’s observatories, using their own private observational stations. For example, al-Battānī observed for many years in Raqqa (in northern Syria); the Banū Mūsā brothers observed for about thirty years from their own properties in Baghdad and the nearby city of Samarra; the Banū Amājūr family, including the father, two sons, and a freed slave, observed over a long period and made their own zījs; and Sharf al-Dawla built an observatory in the garden of his palace in Baghdad.
From the mid-10th to the mid-13th century, observatories or observational stations were built all over the Islamic territories, with various observational instruments and to perform different astronomical programs. In the 950s al-Sūfī conducted observations in Rayy (near Tehran) and Shiraz; in the late 10th century Abū‘l Wafā al-Būzjānī observed from Baghdad, and observed a lunar eclipse simultaneously with al-Bīrūnī while the latter was in Khwarizm (in modern Turkmenistan); in 994 al-Khujandī measured the obliquity of the ecliptic in Rayy using a sextant about 20m in radius; in the 970s Ibn Yūnus started an extended observational program in Cairo which he explains in his zīj; in the late 10th century and the first two decades of the 11th century al-Bīrūnī conducted observations for more than thirty years in Khurasan (eastern Iran); in the late 11th century ‘Umar al-Khayyām used an observatory in Isfahan, Iran, for about 18 years where he prepared a zīj and supervised the calendar reform project for the Seljuk ruler, Malik Shāh; and finally Sā ‘id al-Andalusī and Ibn al-Zarqāllu undertook a long-term observational program in Spain in the 11th century.
However, two observatories in the Islamic period occupy a special place in the history of astronomy: the Maragha Observatory, built in 1259 in northern Iran under the patronage of Hūlāgū (a grandson of the Mongol conqueror Genghis Khan); and the Samarqand Observatory, founded by Ulugh Beg (a grandson of Tamerlane) in 1424. The scale of the observational instruments in these two observatories, the importance of their observational programmes, their institutional setting, and the number of affiliated astronomers and mathematicians, combine to make these two institutions unique in the history of medieval astronomy.
The Samarqand observatory, which was based upon ideas from the Maragha Observatory, in turn became a model for an observatory built by Taqī al-Dīn in Istanbul in 1575 and the Jantar Mantar observatories in north India in the 1720s. After the fall of Ulugh Beg’s dynasty in the 1450s, a number of scholars in Ulugh Beg’s circle emigrated to the newly born Ottoman Empire, where they strongly influenced scientific developments. Taqī al-Dīn, the court astronomer of Sultan Murad III (reign 1574-95), established an observatory in Istanbul, something the Turkish Sultans had dreamed of ever since they conquered Constantinople in 1453. About fifteen astronomers helped to build and use the instruments, whose purpose was to produce a new zīj. However, after two years the great comet of 1577 appeared, which Taqī al-Dīn interpreted as a sign that the Turkish army would be victorious against Persia. Although the Persian army was defeated in the war, the Turkish troops also suffered heavy losses. In the same year several dignitaries died within short intervals, and there was also a plague. Referring to these unpredicted horrifying events, the Sultan believed that the comet appeared because of the establishment of the observatory and that it would go away if its cause (the observatory) were removed. As a result, the observatory was demolished at once, before Taqī al-Dīn was able to finalize his zīj.
The Jantar Mantar observatories built by Jai Singh in northern India between 1724 and 1734, although built after the invention of the telescope, continued the Islamic-Persian tradition of monumental observatory building and were greatly inspired by the Samarqand Observatory.
- InfoVersion: 21
Status: PUB
Date: 2017-11-10 06:46:56
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Theoretical astronomy
In addition to observational and computational astronomy, Muslim astronomers had a special interest in creating a clear picture of the universe in its physical sense. It was generally accepted that the earth was located at the centre of the universe, with all celestial bodies moving uniformly around it. Aristotle had argued that the celestial region consisted of a series of concentric spheres (or ‘orbs’) with the earth at the centre. Each of the planets, for example, moved at a constant rate around one of these orbs. However, observational data did not support this picture: all celestial bodies from the sun and the moon to the planets and stars manifested different short-term or secular non-uniform motions. To explain these observations, non-concentric models of planetary motions had been developed in the 3rd and 2nd centuries BC, culminating in Ptolemy’s model of the planetary motions. This preserved the concentric orbs but included other eccentric orbs and epicycles embedded in each orb. According to Ptolemy, the uniform motion of a planet or the centre of an epicycle occurred around a point called the equant which did not coincide with the earth. With this innovation, the observations and the mathematical models of the planetary motions became compatible, but the physical structure of the universe became unclear. The problem was simple: given that the eccentric orbs, epicycles and equant were only mathematical devices to make the planetary motions calculable, what was the true physical configuration of the celestial spheres? Even Ptolemy was not explicit in his treatment of the universe: in the Almagest he merely describes the motions and models mathematically, while in his Planetary Hypothesis he talks about the configuration of the spheres without referring to problematic premises that underlie his mathematical models.
Critiques of Ptolemy started to appear soon after Muslim astronomers became familiar with the Ptolemaic system. Doubts concerning either Ptolemy’s observational data or his description of the cosmos became common in Islam. The main challenge was to create a configuration (hay‘a) of the universe that satisfied both observational and physical principles. The main goal, in other words, was to develop models involving uniform motions around the centre of the universe—the earth—that were compatible with observations.


Fig. 3. Left/Top: Tūsī’s couple. Imagine two spheres internally tangent at one point (C), the diameter of the small sphere being equal to half of the other. If the small sphere uniformly moves twice (2α) as fast as the big sphere but in the opposite direction, the common point D will move back and forth along AB. In other words, the uniform circular motions of the two spheres create a linear motion. By choosing a Tūsī’s couple with the right dimensions and speeds of the two revolving spheres, and attaching it to a given sphere, one can produce the observed non-uniform motion of a particular planet around the central earth, even though the motion of the revolving spheres is uniform. Therefore, both observation and physical principles are preserved. © Tofigh Heidarzadeh. Right/Bottom: Tūsī’s diagram of the couple, showing the oscillation of a given point along the diameter of the big circle. After Tūsī couple from Vat. Arabic ms 319, commons.wikimedia.org. Creative Commons Licence
Solving this problem occupied the minds of several Muslim astronomers, among them Ibn al-Haytham, Ibn-Sīnā’s student Abū ‘Ubeyd Jūzjānī, Ibn Rūshd, and Ibn Bājja. However, it was Nasīr al-Dīn al-Tūsī who developed a revolutionary solution to eliminate the equant. Tūsī introduced an arrangement in which the circular motions of two spheres produced a linear motion displacing a point (for example the centre of an epicycle) closer to or further from a central point. This arrangement (called Tūsī’s couple), which was able to produce non-uniform motions from concentric uniform motions, was a key concept in the development of non-Ptolemaic models. Tūsī’s contemporaries Mu‘ayyad al-Dīn al-‘Urdī and Qutb al-Dīn Shīrazī also developed innovative non-Ptolemaic models, and the tradition continued with further models produced by Alī Al-Qūshjī (of Samarqand Observatory) and Ibn al-Shātir (1304-75), the timekeeper of the Umayyad Mosque in Damascus.
Copernicus repeatedly used concepts developed by Tūsī and his followers and colleagues. In De revolutionibus he employed Tūsī’s couple to create the variation in the obliquity of the ecliptic and to produce an oscillation in the orbital planes of planets. In the Commentariolus Copernicus uses al-‘Urdī and Ibn al-Shātir’s models to develop his own models for planetary longitude. Copernicus’s model for the lunar motions is almost the same as the model proposed by Ibn al-Shātir. Copernicus probably became aware of Muslim non-Ptolemaic models, especially those developed by Tūsī and his followers, when he was studying in Italy, where there was easier access to Arabic texts.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.
- InfoVersion: 21
Status: PUB
Date: 2017-11-10 06:46:56
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Theoretical astronomy
In addition to observational and computational astronomy, Muslim astronomers had a special interest in creating a clear picture of the universe in its physical sense. It was generally accepted that the earth was located at the centre of the universe, with all celestial bodies moving uniformly around it. Aristotle had argued that the celestial region consisted of a series of concentric spheres (or ‘orbs’) with the earth at the centre. Each of the planets, for example, moved at a constant rate around one of these orbs. However, observational data did not support this picture: all celestial bodies from the sun and the moon to the planets and stars manifested different short-term or secular non-uniform motions. To explain these observations, non-concentric models of planetary motions had been developed in the 3rd and 2nd centuries BC, culminating in Ptolemy’s model of the planetary motions. This preserved the concentric orbs but included other eccentric orbs and epicycles embedded in each orb. According to Ptolemy, the uniform motion of a planet or the centre of an epicycle occurred around a point called the equant which did not coincide with the earth. With this innovation, the observations and the mathematical models of the planetary motions became compatible, but the physical structure of the universe became unclear. The problem was simple: given that the eccentric orbs, epicycles and equant were only mathematical devices to make the planetary motions calculable, what was the true physical configuration of the celestial spheres? Even Ptolemy was not explicit in his treatment of the universe: in the Almagest he merely describes the motions and models mathematically, while in his Planetary Hypothesis he talks about the configuration of the spheres without referring to problematic premises that underlie his mathematical models.
Critiques of Ptolemy started to appear soon after Muslim astronomers became familiar with the Ptolemaic system. Doubts concerning either Ptolemy’s observational data or his description of the cosmos became common in Islam. The main challenge was to create a configuration (hay‘a) of the universe that satisfied both observational and physical principles. The main goal, in other words, was to develop models involving uniform motions around the centre of the universe—the earth—that were compatible with observations.


Fig. 3. Left/Top: Tūsī’s couple. Imagine two spheres internally tangent at one point (C), the diameter of the small sphere being equal to half of the other. If the small sphere uniformly moves twice (2α) as fast as the big sphere but in the opposite direction, the common point D will move back and forth along AB. In other words, the uniform circular motions of the two spheres create a linear motion. By choosing a Tūsī’s couple with the right dimensions and speeds of the two revolving spheres, and attaching it to a given sphere, one can produce the observed non-uniform motion of a particular planet around the central earth, even though the motion of the revolving spheres is uniform. Therefore, both observation and physical principles are preserved. © Tofigh Heidarzadeh. Right/Bottom: Tūsī’s diagram of the couple, showing the oscillation of a given point along the diameter of the big circle. After Tūsī couple from Vat. Arabic ms 319, commons.wikimedia.org. Creative Commons Licence
Solving this problem occupied the minds of several Muslim astronomers, among them Ibn al-Haytham, Ibn-Sīnā’s student Abū ‘Ubeyd Jūzjānī, Ibn Rūshd, and Ibn Bājja. However, it was Nasīr al-Dīn al-Tūsī who developed a revolutionary solution to eliminate the equant. Tūsī introduced an arrangement in which the circular motions of two spheres produced a linear motion displacing a point (for example the centre of an epicycle) closer to or further from a central point. This arrangement (called Tūsī’s couple), which was able to produce non-uniform motions from concentric uniform motions, was a key concept in the development of non-Ptolemaic models. Tūsī’s contemporaries Mu‘ayyad al-Dīn al-‘Urdī and Qutb al-Dīn Shīrazī also developed innovative non-Ptolemaic models, and the tradition continued with further models produced by Alī Al-Qūshjī (of Samarqand Observatory) and Ibn al-Shātir (1304-75), the timekeeper of the Umayyad Mosque in Damascus.
Copernicus repeatedly used concepts developed by Tūsī and his followers and colleagues. In De revolutionibus he employed Tūsī’s couple to create the variation in the obliquity of the ecliptic and to produce an oscillation in the orbital planes of planets. In the Commentariolus Copernicus uses al-‘Urdī and Ibn al-Shātir’s models to develop his own models for planetary longitude. Copernicus’s model for the lunar motions is almost the same as the model proposed by Ibn al-Shātir. Copernicus probably became aware of Muslim non-Ptolemaic models, especially those developed by Tūsī and his followers, when he was studying in Italy, where there was easier access to Arabic texts.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.
- InfoVersion: 4
Status: PUB
Date: 2017-11-10 06:48:44
Author(s): Tofigh Heidarzadeh with contributions by Clive Ruggles
Select bibliography
- Dallal, Ahmad (1999). Science, medicine, and technology: the making of a scientific culture, in The Oxford History of Islam, edited by John L. Eposito, pp. 155-213. Oxford: Oxford University Press.
- Heidarzadeh, Tofigh (2005). Patronage, networks and migration: Turco-Persian scholarly exchanges in the 15th, 16th and 17th centuries, Archives Internationales d’Histoire des Sciences 55, 419-434.
- Heidarzadeh, Tofigh (2008). A History of Physical Theories of Comets, from Aristotle to Whipple. Dordrecht: Springer Science and Business Media.
- Kennedy, E.S. (1956). A survey of Islamic astronomical tables, Transactions of the American Philosophical Society 42:2, 121-177.
- King, David A (1990). Science in the service of religion: the case of Islam, Impact of Science on Society 159, 245-262.
- King, David A (1999). World-Maps for Finding the Direction and Distance to Mecca. Leiden: Brill.
- King, David A., J. Samsó and B. R. Goldstein (2001). Astronomical handbooks and tables from the Islamic world (750-1900), Suhayl 2, 12-105.
- Lindberg, David C. (1992). The Beginnings of Western Science, The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450. Chicago: University of Chicago Press.
- North, John D. (2008). Cosmos: An Illustrated History of Astronomy and Cosmology. Chicago: University of Chicago Press.
- Pederson, Olaf (1993). Early Physics and Astronomy. Cambridge: Cambridge University Press.
- Saliba, George (1995). A History of Arabic Astronomy: Planetary Theories during the Golden Age of Islam. New York: New York University Press.
- Saliba, George (2007). Islamic Science and the Making of the European Renaissance. Cambridge, MA: MIT Press.
- Sayili, Aydin (1988). The Observatory in Islam. Ankara: Turk Tarih Kurumu Basimevi.
- Swerdlow, Noel (1973). The derivation and first draft of Copernicuss planetary theory. A translation of the Commentariolus with commentary, Proceedings of the American Philosophical Society 117, 423-512.
- Wellesz, Emmy (1965). An Islamic Book of Constellations (Bodleian Picture Book, no. 13). Oxford: Bodleian Library.
The contents of this page are based upon text in the ICOMOS-IAU Thematic Study no. 1 (2010). Original text © Clive Ruggles, Michel Cotte and the contributing authors.

